斐波那契数列

斐波那契数列 (意大利语： Successione di Fibonacci)，又称黄金分割数列、费波那西数列、费波拿契数、费氏数列，指的是这样一个数列：1、1、2、3、5、8、13、21、……在数学上，斐波那契数列以如下被以递归的方法定义：F1=1，F2=1，Fn=F(n-1) + F(n-2) (n>2，n∈N*)，使用递归实现如下:

public static int fib(int n) {
    if (n == 1 || n == 2) { return 1; }

    return fib(n-1) + fib(n-2);
}

求 fib(6) 斐波那契数列的递归过程如图:

> 重叠子问题 (Overlap subproblem): 把大问题被分解为多个小问题进行求解，小问题重复的出现多次。

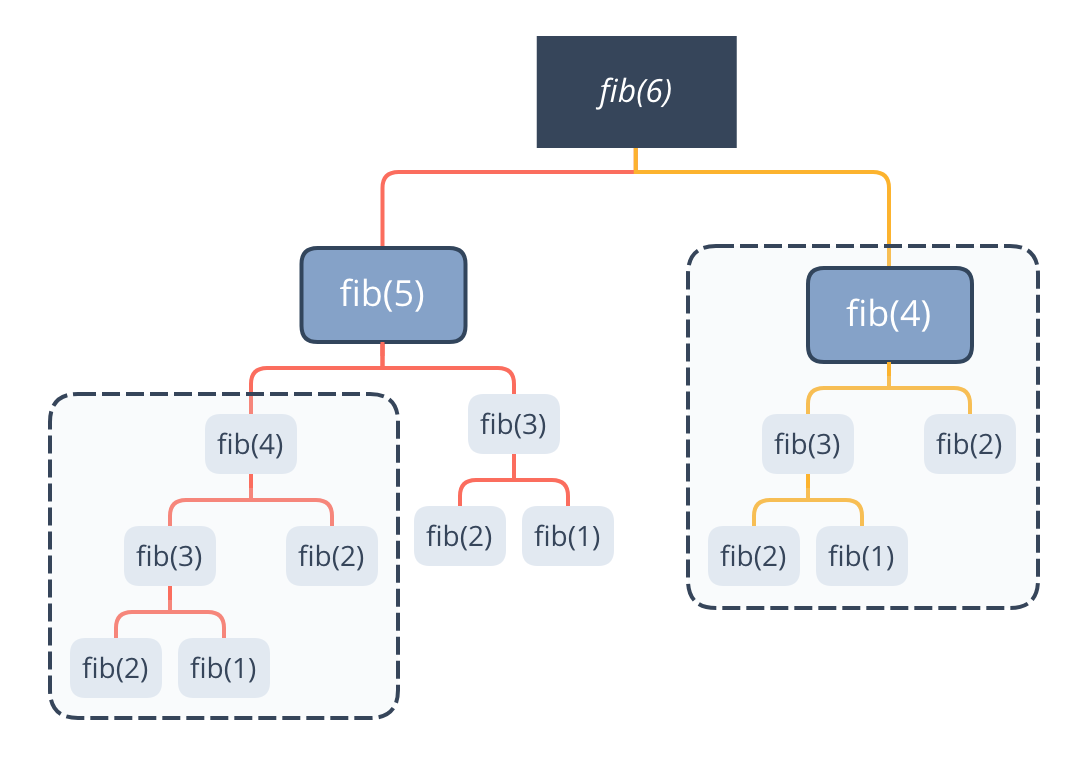
从图中可以看到，计算 fib(6) 时，fib(4) 被计算了 2 次，fib(3) 被计算了 3 次，产生了大量的重复计算。如果第一次计算 fib(3), fib(4) 时先把他们的结果保存起来，再次使用它们的时候使用查表的方式直接得到结果就可以避免大量重复计算。

数组 solution 保存斐波那契数列，第 N 个下标存储第 N 个斐波那契数:

public static void main(String[] args) throws IOException {
    int[] solution = new int[21];
    solution[1] = solution[2] = 1;

    System.out.println(fib(20, solution));
}

public static int fib(int n, int[] solution) {
    if (solution[n] != 0) { return solution[n]; }

    return solution[n] = fib(n-2, solution) + fib(n-1, solution);
}

为了比较这 2 种方法的计算量，在 fib 函数中使用一个计数器，调用一次 fib 函数计数器就加 1:

• 计算 10 项斐波那契数列
  • 第一种方式调用了 109 次 fib 函数
  • 缓存子问题解的方式调用了 17 次 fib 函数
• 计算 20 项斐波那契数列
  • 第一种方式调用了 13529 次 fib 函数
  • 缓存子问题解的方式调用了 37 次 fib 函数
• 计算 30 项斐波那契数列
  • 第一种方式调用了 1664079 次 fib 函数
  • 缓存子问题解的方式调用了 57 次 fib 函数
• 计算 40 项斐波那契数列
  • 第一种方式调用了 204668309 次 fib 函数
  • 缓存子问题解的方式调用了 77 次 fib 函数

可见，缓存子问题的方式虽然额外使用了点空间，但是大大的减少了计算量，极大的提高了运算效率。