Content Table
2024-10-12

Redis Auth 授权

Redis 授权有 2 中方式:

  • 只使用密码。
  • 用户名 + 密码。

只使用密码

在配置文件 redis.conf 中搜索 requirepass 或 # requirepass，将该行的注释符号 # 去掉，并在等号后面输入你想要设置的密码。例如：

1
requirepass Passw0rd

客户端访问:

1
2
3
4
5
6
# 命令中使用密码
redis-cli -h localhost -p 6379 -a Passw0rd

# 登录后输入密码
redis-cli -h localhost -p 6379
auth Passw0rd

阅读全文

2023-12-19

VxeTable 数组结构

VxeTable 主要是支持虚拟滚动。

简单使用

表格的数据为对象的数组，手动固定列 (也可以使用循环)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
<template>
    <vxe-table border :data="tableData">
        <vxe-column type="seq" width="60"/>

        <!-- 没有使用插槽，列的值自动为行对象中属性为 name 的属性值 -->
        <vxe-column field="name" title="Name"/>
        <vxe-column field="gender" title="gender"/>
        <vxe-column field="age" title="Age"/>
    </vxe-table>
</template>

<script setup lang="ts">
const tableData = [
    { id: 10001, name: 'Test1', role: 'Develop', gender: 'Man', age: 28, address: 'test abc' },
    { id: 10002, name: 'Test2', role: 'Test', gender: 'Women', age: 22, address: 'Guangzhou' },
    { id: 10003, name: 'Test3', role: 'PM', gender: 'Man', age: 32, address: 'Shanghai' },
    { id: 10004, name: 'Test4', role: 'Designer', gender: 'Women', age: 24, address: 'Shanghai' }
];
</script>

阅读全文

2023-03-29

任务队列、异步并发

使用任务队列、异步、并发且限制并发数量的主要控制流程，这个模型在大文件分片上传时能够用到。

框架代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
// 异步、并发、最大并发数执行任务。
const MAX_EXECUTING_TASK_COUNT = 3; // 任务执行时的最大并发数
let taskQueue = []; // 任务队列

let totalTaskCount     = 0; // 总的任务数量
let finishedTaskCount  = 0; // 已完成的任务数量
let executingTaskCount = 0; // 正在执行的任务数量

start();

// 开始执行。
function start() {
    buildTaskQueue();
    totalTaskCount = taskQueue.length;

    // 开启多个任务并发执行。
    for (let i = 0; i < MAX_EXECUTING_TASK_COUNT; i++) {
        startTask();
    }
}

// 构建任务队列，例如从服务器获取任务信息。
function buildTaskQueue() {
    taskQueue = [1, 2, 3, 4, 5, 6, 7, 8, 9];
}

/**
 * 开始任务。
 *
 * @returns 无。
 */
function startTask() {
    /*
     逻辑:
     1. 如果超过允许的最大并发任务数则不开启新的任务。
     2. 如果任务队列为空则不开启新的任务。
     3. 从任务队列里获取一个任务然后执行:
        3.1 正在执行的任务数 +1。
        3.2 使用 Promise 执行异步耗时任务。
     4. 每个任务执行结束后调用 onTaskFinish()，在其中决定执行新的任务还是任务所有任务都执行结束。
     */

    // [1] 如果超过允许的最大并发任务数则不开启新的任务。
    if (executingTaskCount >= MAX_EXECUTING_TASK_COUNT) {
        return;
    }
    // [2] 如果任务队列为空则不开启新的任务。
    if (taskQueue.length == 0) {
        return;
    }

    // [3] 从任务队列里获取一个任务然后执行:
    // [3.1] 正在执行的任务数 +1。
    executingTaskCount++;
    let t = taskQueue.shift();
    let delay = parseInt(200 + Math.random() * 2000);

    console.log(`[开始] 执行任务: ${t}, 耗时: ${delay} 毫秒`);

    // [3.2] 使用 Promise 执行异步耗时任务。
    let p = new Promise((resolve, reject) => {
        // 传输文件 (异步耗时任务)
        setTimeout(()=>{
            resolve(t);
        }, delay);
    });

    // [4] 每个任务执行结束后调用 onTaskFinish()，在其中决定执行新的任务还是任务所有任务都执行结束。
    p.then((r) => {
        onTaskFinish(t);
    }).catch(err => {
        onTaskFinish(t);
        console.err(err);
    })
}

/**
 * 任务结束 (成功或失败)。
 *
 * @param {Json} task 任务。
 * @returns 无。
 */
function onTaskFinish(task) {
    console.log(`[完成] 执行任务: ${task}, 剩下任务数: ${taskQueue.length}`);
    finishedTaskCount++;
    executingTaskCount--;

    if (finishedTaskCount == totalTaskCount) {
        // 任务都执行结束。
        console.log("所有任务执行完成 ✔️✔️✔️");
    } else {
        // 一个任务结束，执行新的任务。
        startTask();
    }
}

阅读全文

2023-03-05

Hexo 使用 Mermaid

Hexo 主题中使用 Mermaid 按照官方的介绍文档会报错:

  • mermaid.js 和 require.js 冲突，需要在 require.js 前引入。
  • 配置读取失败，theme.mermaid 为未定义。

Hexo 主题中使用 Mermaid 的步骤可以写死为:

  1. 在 head.ejs 中引入 Mermaid:

    1
    2
    3
    4
    5
    6
    <!-- mermaid.js 需要在 require.js 前面加载 -->
    <script src='https://unpkg.com/mermaid@8.7.0/dist/mermaid.min.js'></script>

    <script src="/js/jquery.min.js"></script>
    <script src="/js/require.min.js"></script>
    <script src="/js/main.js"></script>

  2. 在 after-footer.ejs 中初始化 Mermaid:

    1
    2
    3
    4
    5
    <script>
      if (window.mermaid) {
        mermaid.initialize({theme: 'dark'});
      }
    </script>

示例:

1
2
3
4
5
flowchart TB
    A[Client 分片上传文件] -- 发送 --> S1[分片 1] & S2[分片 2] & S3[分片 3]
    S1 & S2 & S3 --> Gateway
    Gateway --> DSC1
    Gateway -- 保证所有分片都发送到 --> DSC2

效果:

flowchart TB
    A[Client 分片上传文件] -- 发送 --> S1[分片 1] & S2[分片 2] & S3[分片 3]
    S1 & S2 & S3 --> Gateway
    Gateway --> DSC1
    Gateway -- 保证所有分片都发送到 --> DSC2
2023-02-17

JSON 日志显示为表格

日志系统输出的是 JSON 格式的日志，每行一个 JSON 对象，例如:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
{"func":"newdtagent/service.(*WatchdogService).UpdateAgent():63","level":"info","msg":"升级 Agent","time":"2023-02-17 14:03:42","version":"v1.0"}
{"func":"newdtagent/service.(*WatchdogService).doUpdateAgent():60","level":"info","msg":"下载 Agent","time":"2023-02-17 14:03:42","version":"v1.0"}
{"autoServiceAddr":"10.10.10.36:8290","func":"newdtagent/service.(*WatchdogService).downloadAgent():289","level":"warning","msg":"[成功] 下载 Agent 成功","time":"2023-02-17 14:03:53","url":"http://10.10.10.36:8290/api/agents/versions/v1.0/downloadInPartition"}
{"count":1,"error":"不能升级，正在执行任务: RunningJobsCount: 1, UploadingFileCount: 0","func":"newdtagent/service.(*WatchdogService).doUpdateAgent.func3():124","level":"warning","msg":"尝试升级 Agent...","time":"2023-02-17 14:03:53"}
{"count":2,"error":"不能升级，正在执行任务: RunningJobsCount: 1, UploadingFileCount: 0","func":"newdtagent/service.(*WatchdogService).doUpdateAgent.func3():124","level":"warning","msg":"尝试升级 Agent...","time":"2023-02-17 14:03:58"}
{"count":3,"error":"不能升级，正在执行任务: RunningJobsCount: 1, UploadingFileCount: 0","func":"newdtagent/service.(*WatchdogService).doUpdateAgent.func3():124","level":"warning","msg":"尝试升级 Agent...","time":"2023-02-17 14:04:03"}
{"count":4,"error":"不能升级，正在执行任务: RunningJobsCount: 1, UploadingFileCount: 0","func":"newdtagent/service.(*WatchdogService).doUpdateAgent.func3():124","level":"warning","msg":"尝试升级 Agent...","time":"2023-02-17 14:04:08"}
{"count":5,"error":"不能升级，正在执行任务: RunningJobsCount: 1, UploadingFileCount: 0","func":"newdtagent/service.(*WatchdogService).doUpdateAgent.func3():124","level":"warning","msg":"尝试升级 Agent...","time":"2023-02-17 14:04:13"}
{"count":6,"error":"不能升级，正在执行任务: RunningJobsCount: 1, UploadingFileCount: 0","func":"newdtagent/service.(*WatchdogService).doUpdateAgent.func3():124","level":"warning","msg":"尝试升级 Agent...","time":"2023-02-17 14:04:18"}
{"count":7,"error":"不能升级，正在执行任务: RunningJobsCount: 1, UploadingFileCount: 0","func":"newdtagent/service.(*WatchdogService).doUpdateAgent.func3():124","level":"warning","msg":"尝试升级 Agent...","time":"2023-02-17 14:04:23"}
{"error":"Get \"http://127.0.0.1:12301/api/stats\": dial tcp 127.0.0.1:12301: connect: connection refused","func":"newdtagent/service.(*WatchdogService).doGetAgentStats():34","level":"warning","msg":"[错误] 获取 Agent 状态失败","time":"2023-02-17 14:04:28"}
{"func":"newdtagent/service.(*WatchdogService).doStopAgent.func1():170","level":"info","msg":"[成功] 退出 Agent 成功","time":"2023-02-17 14:04:28"}
{"error":"Get \"http://127.0.0.1:12301/api/stats\": dial tcp 127.0.0.1:12301: connect: connection refused","func":"newdtagent/service.(*WatchdogService).doGetAgentStats():34","level":"warning","msg":"[错误] 获取 Agent 状态失败","time":"2023-02-17 14:04:28"}
{"func":"newdtagent/service.(*WatchdogService).doStartAgent.func1():239","level":"info","msg":"[成功] 启动 Agent 成功","time":"2023-02-17 14:04:30"}

阅读全文

2022-12-07

Go 实现超时处理

Go 通常可以使用以下 3 种方式实现超时:

  • Timeout Context 实现超时
  • Cancel Context 实现超时
  • 手动操作 channel 实现超时

推荐使用 Cancel Context 的方式实现超时功能，因为区分是正常结束还是超时结束比较容易。

Timeout Context 实现超时

TimeoutContext 的特点:

  • 超时会自动往 Done() 返回的 channel 里写入数据。
  • 手动调用 CancelFunc 也会往 Done() 返回的 channel 里写入数据。
  • 需要对 Context.Err() 进行判断区分是正常结束还是自动超时结束。

案例代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
package main

import (
    "context"
    "fmt"
    "math/rand"
    "time"
)

func main() {
    rand.Seed(time.Now().UTC().UnixNano())
    ctx, cancel := context.WithTimeout(context.Background(), time.Second*3)

    // 异步请求
    go func(cancel func()) {
        defer cancel()

        fmt.Println("Query Start...")

        // 模拟耗时请求，耗时随机 1 到 6 秒
        d := 1 + rand.Intn(6) // 1..6
        fmt.Printf("Query use %dS\n", d)
        time.Sleep(time.Second * time.Duration(d))
        fmt.Println("Query Finished!")
    }(cancel)

    // [*] 等待超时结束或者请求提前结束
    <-ctx.Done()

    // 1. 请求结束, Error: context canceled
    // 2. 请求结束, Error: context deadline exceeded
    fmt.Printf("请求结束, Error: %v\n", ctx.Err())
}

正常输出:

1
2
3
4
Query Start...
Query use 2S
Query Finished!
请求结束, Error: context canceled

超时输出:

1
2
3
Query Start...
Query use 4S
请求结束, Error: context deadline exceeded

阅读全文

2022-07-15

Watchdog

可以使用 watchdog 控制某些耗时操作的超时时间，当超时的时候执行指定的操作，例如中断线程、重置 Redis key 的超时时间等。Apache 的 commons-exec 包中提供了 watchdog 的实现供我们使用 (源码为文章后面的 Watchdog.java)。

According to wikipedia - watchdog is an electronic timer that is used to detect and recover from computer malfunctions.

案例演示

下面的例子执行拼接字符串的耗时操作，定义了一个 watchdog，超时时间为 1S，超时后 watchdog 中断线程结束字符串拼接操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import org.apache.commons.exec.Watchdog;

import java.text.SimpleDateFormat;
import java.util.Date;
import java.util.concurrent.TimeUnit;

public class Test {
    private static final SimpleDateFormat formatter = new SimpleDateFormat("hh:mm:ss");

    public static void main(String[] args) {
        Thread thread = new Thread(() -> {
            // 创建 watchdog
            Thread t = Thread.currentThread();
            Watchdog watchdog = new Watchdog(TimeUnit.SECONDS.toMillis(1));

            // 超时且未关闭 watchdog 时执行的操作
            watchdog.addTimeoutObserver(w -> {
                System.out.println("Watchdog trigger");
                t.interrupt();
            });

            // 启动 watchdog
            watchdog.start();

            // 执行耗时任务，超时的时候当前线程的 isInterrupted() 为 true，结束循环
            System.out.println("开始时间: " + formatter.format(new Date()));
            int count = 0;
            StringBuilder sb = new StringBuilder();
            while (!t.isInterrupted() && count++ < 10000) {
                sb.append(count);
            }
            System.out.printf("结束时间: %s，循环次数: %d", formatter.format(new Date()), count);

            // 关闭 watchdog
            watchdog.stop();
        });

        thread.start();
    }
}

输出:

1
2
3
开始时间: 01:51:40
Watchdog trigger
结束时间: 01:51:41，循环次数: 48060741

阅读全文

2022-05-04

Monterey 混合 VPN 访问公司内网

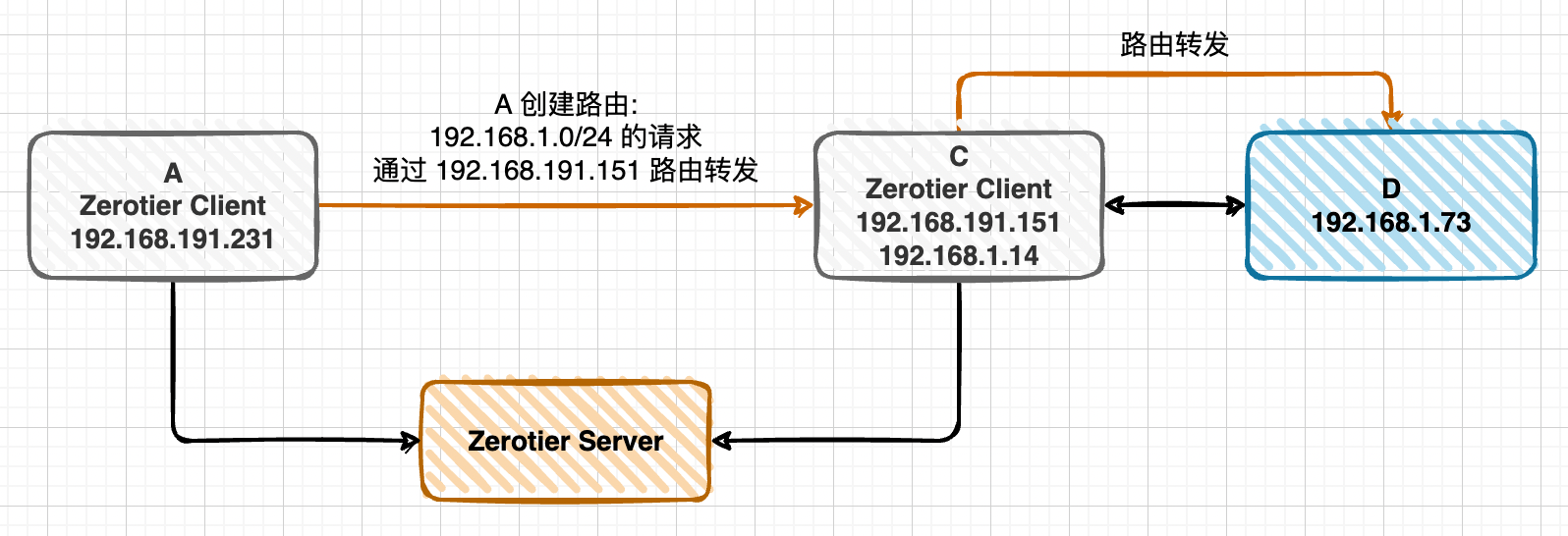
在 OSX Monterey 使用 VPN 中介绍了 Monterey 使用 L2TP-IpSpec VPN 的问题，并且使用 Windows Server 2016 进行中转处理的方案，虽然勉强能用，但是不够方便，本文中介绍了几种其他方案:

  • 方案一、Zerotier
  • 方案二、Wireguard
  • 方案三、Wireguard + Zerotier

由于各种原因最终使用了方案三，本地能够直接访问公司内网了，且速度能够接受，比使用 Windows Server 2016 的方案更好，但技术上也复杂不少。当有内网可使用 Wireguard 的机器时再切换为方案二，不考虑方案一是因为跨电信运营商时太慢。

方案一、Zerotier

阅读全文

2022-04-26

Mac 终端打造

Mac 的终端打造主要综合使用 iTerm + Shuttle + Expect 这三个软件:

  • iTerm: 替代系统自带的 Terminal
  • Shuttle: 为快捷命令菜单，点击后在 iTerm 中执行相应的命令，可用于管理常用命令和管理 SSH 主机
  • Expect: masOS 自带了 Expect，可实现 SSH 自动登录

iTerm

iTerm 可匹配内容进行高亮显示、按下快捷键后窗口从屏幕上方滚动下来，请参考 iTerm 设置。

如下图设置配置 iTerm 的主题，请参考 Mac Terminal Powerlevel。

阅读全文

2022-03-28

Java 执行命令

使用 Java 执行命令，可以:

下面以执行 ls -l / 为例演示相关代码。

ProcessBuilder

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public static void executeCommandUsingProcessBuilder() throws Exception {
    ProcessBuilder pb = new ProcessBuilder("ls", "-l", "/");
    Process p = pb.start();

    StringBuilder sbOk = new StringBuilder();
    StringBuilder sbError = new StringBuilder();

    // 读取正常输出
    BufferedReader okReader = new BufferedReader(new InputStreamReader(p.getInputStream()));
    String okLine = null;
    while ((okLine = okReader.readLine()) != null) {
        sbOk.append(okLine).append("\n");
    }

    // 读取错误输出
    BufferedReader errorReader = new BufferedReader(new InputStreamReader(p.getErrorStream()));
    String errorLine = null;
    while ((errorLine = errorReader.readLine()) != null) {
        sbError.append(errorLine).append("\n");
    }

    System.out.println(sbOk.toString());
    System.out.println(sbError.toString());
}

疑问: 虽然如上能正常的获取到进程的正常和错误输出，慎用，因为缓冲区写满了的时候，由于没有读取其中的数据，无法继续写入数据，导致线程阻塞，对外现象就是进程无法停止，也不占资源，什么反应也没有，参考使用 JDK 写法。

阅读全文