Content Table
2017-06-24

JS 绘制平滑曲线

本文介绍在 JS 中绘制平滑曲线的实现，调用下面的函数 drawSmoothCurve() 即可。默认曲线的 2 个顶点之间被分割为 16 个小线段来拟合曲线，下图展示了 tension 为 0.3，0.5，0.7 时的曲线效果，tension 并不是越大越好，默认的 0.5 大多数时候就不错。

算法来自于 How to draw smooth curve through N points using javascript HTML5 canvas?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
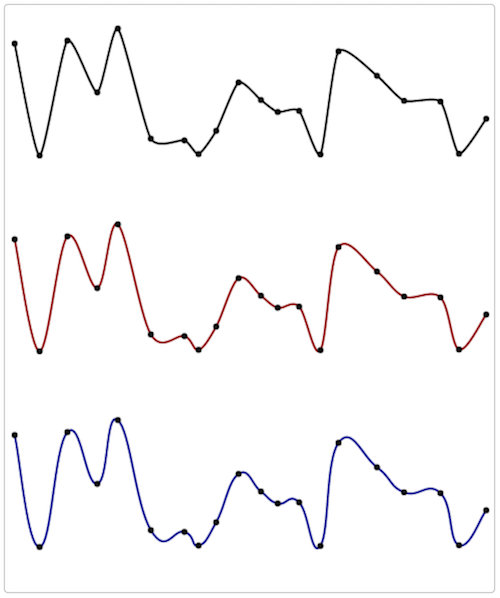
<!DOCTYPE html>
<html>

<head>
    <meta charset="utf-8">
    <title>绘制平滑曲线</title>
    <script src="http://cdn.bootcss.com/jquery/3.2.1/jquery.min.js"></script>
    <style media="screen">
        canvas {
            border: 1px solid #BBB;
            border-radius: 4px;
        }
    </style>
</head>

<body>
    <canvas id="canvas" width="500" height="600">Your browser does not support canvas.</canvas>

    <script>
        var canvas = $('#canvas').get(0);
        var context = canvas.getContext('2d');
        context.lineWidth = 2;

        // 曲线顶点坐标数组，points[i] 是第 i 个点的 x 坐标，points[i+1] 是第 i 个点的 y 坐标
        var points = [];
        var showPoints = true;

        for (var x = 10; x < canvas.width;) {
            var dx = Math.random() * 30 + 10;
            var y  = Math.random() * 150 + 20;
            points.push(x);
            points.push(y);
            x += dx;
        }

        // tension 不一样，对比效果
        drawSmoothCurve(context, points, showPoints, 0.3);

        context.strokeStyle = 'darkred';
        context.translate(0, 200);
        drawSmoothCurve(context, points, showPoints); // tension 默认为 0.5，效果不错

        context.strokeStyle = 'darkblue';
        context.translate(0, 200);
        drawSmoothCurve(context, points, showPoints, 0.7);

        /**
         * 绘制平滑曲线。
         *
         * @param  {Object}  context Canvas 的 context
         * @param  {Array}   points  曲线顶点坐标数组，
         *                           points[i+0] 是第 i 个点的 x 坐标，
         *                           points[i+1] 是第 i 个点的 y 坐标
         * @param  {Boolean} showPoints 是否绘制曲线的顶点
         * @param  {Float}   tension    密集程度，默认为 0.5
         * @param  {Boolean} closed     是否创建闭合曲线，默认为 false
         * @param  {Int}     numberOfSegments 平滑曲线 2 个顶点间的线段数，默认为 16
         * @return 无返回值
         */
        function drawSmoothCurve(context, points, showPoints, tension, closed, numberOfSegments) {
            drawLines(context, createSmoothCurvePoints(points, tension, closed, numberOfSegments));
            showPoints && drawPoints(context, points);
        }

        /**
         * 使用传入的曲线的顶点坐标创建平滑曲线的顶点。
         *
         * @param  {Array}   points  曲线顶点坐标数组，
         *                           points[i+0] 是第 i 个点的 x 坐标，
         *                           points[i+1] 是第 i 个点的 y 坐标
         * @param  {Float}   tension 密集程度，默认为 0.5
         * @param  {Boolean} closed  是否创建闭合曲线，默认为 false
         * @param  {Int}     numberOfSegments 平滑曲线 2 个顶点间的线段数，默认为 16
         * @return {Array}   平滑曲线的顶点坐标数组
         */
        function createSmoothCurvePoints(points, tension, closed, numberOfSegments) {
            if (points.length < 4) { return points; }

            // use input value if provided, or use a default value
            tension = tension ? tension : 0.5;
            closed = closed ? true : false;
            numberOfSegments = numberOfSegments ? numberOfSegments : 16;

            var ps = points.slice(0), // clone array so we don't change the original
                result = [], // result points
                x, y, // our x,y coords
                t1x, t2x, t1y, t2y, // tension vectors
                c1, c2, c3, c4, // cardinal points
                st, t, i; // steps based on number of segments

            // The algorithm require a previous and next point to the actual point array.
            // Check if we will draw closed or open curve.
            // If closed, copy end points to beginning and first points to end
            // If open, duplicate first points to befinning, end points to end
            if (closed) {
                ps.unshift(points[points.length - 1]);
                ps.unshift(points[points.length - 2]);
                ps.unshift(points[points.length - 1]);
                ps.unshift(points[points.length - 2]);
                ps.push(points[0]);
                ps.push(points[1]);
            } else {
                ps.unshift(points[1]); // copy 1st point and insert at beginning
                ps.unshift(points[0]);
                ps.push(points[points.length - 2]); // copy last point and append
                ps.push(points[points.length - 1]);
            }

            // 1. loop goes through point array
            // 2. loop goes through each segment between the 2 points + 1e point before and after
            for (i = 2; i < (ps.length - 4); i += 2) {
                // calculate tension vectors
                t1x = (ps[i + 2] - ps[i - 2]) * tension;
                t2x = (ps[i + 4] - ps[i - 0]) * tension;
                t1y = (ps[i + 3] - ps[i - 1]) * tension;
                t2y = (ps[i + 5] - ps[i + 1]) * tension;

                for (t = 0; t <= numberOfSegments; t++) {
                    // calculate step
                    st = t / numberOfSegments;

                    // calculate cardinals
                    c1 = 2 * Math.pow(st, 3) - 3 * Math.pow(st, 2) + 1;
                    c2 = -(2 * Math.pow(st, 3)) + 3 * Math.pow(st, 2);
                    c3 = Math.pow(st, 3) - 2 * Math.pow(st, 2) + st;
                    c4 = Math.pow(st, 3) - Math.pow(st, 2);

                    // calculate x and y cords with common control vectors
                    x = c1 * ps[i] + c2 * ps[i + 2] + c3 * t1x + c4 * t2x;
                    y = c1 * ps[i + 1] + c2 * ps[i + 3] + c3 * t1y + c4 * t2y;

                    //store points in array
                    result.push(x);
                    result.push(y);
                }
            }

            return result;
        }

        function drawLines(context, points) {
            context.beginPath();
            context.moveTo(points[0], points[1]);
            for (i = 2; i < points.length - 1; i += 2) {
                context.lineTo(points[i], points[i + 1]);
            }
            context.stroke();
        }

        function drawPoints(context, points) {
            for (var i = 0; i < points.length - 1; i += 2) {
                context.beginPath();
                context.arc(points[i], points[i + 1], 3, 0, Math.PI * 2);
                context.fill();
            }
        }
    </script>
</body>

</html>