QPainter 提供了绘制线段、矩形、椭圆、圆、圆弧、路径等的函数,如果想绘制正弦 (y=sin(x))、余弦 (y=cos(x)) 的曲线,QPainter 没有提供相应的绘制函数,应该怎么办呢?
李小龙的武术哲学: 以无法为有法,以无限为有限。
数学曲线是连续的,计算机的世界却是离散的,离散的世界使用极限的方式就可以模拟出连续的效果。可以把曲线想象成是一条一条线段连起来形成的图形,这些线段越短,连成的图形就越逼近曲线,这种方法就是线段拟合曲线,学过微积分的同学是不是感觉这个方法很熟悉?
下面以绘制正弦 (y=sin(x)) 曲线为例进行介绍:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| void FittingCurveWidget::paintEvent(QPaintEvent *) {
QPainter painter(this);
painter.setRenderHint(QPainter::Antialiasing);
painter.translate(10, 150);
painter.setPen(QPen(Qt::gray, 1, Qt::DashLine));
painter.drawLine(0, 0, 700, 0);
painter.drawLine(0, -200, 0, 200);
painter.setPen(QPen(Qt::black, 1));
qreal prex = 0, prey = 0;
for (int i = 0; i <= 628; ++i) {
qreal x = i;
qreal y = qSin(i/314.0*M_PI) * 100;
painter.drawLine(prex, prey, x, y);
prex = x;
prey = y;
}
}
|
调用 painter.translate(10, 150) 先把坐标轴向下移动,否则 y 小于 0 的曲线部分看不到,然后绘制坐标轴作为参考。接下来就是使用正弦公式计算坐标,2 个点连成一条线段,当前线段的起点为上一个线段的终点,最后绘制出来的效果如下图。
提示: 计算坐标使用了一个小技巧,把坐标放大了一百倍,这样绘制出来的效果就很明显了,否则绘制 0 到 2PI 的正弦曲线,根本就看不出来。
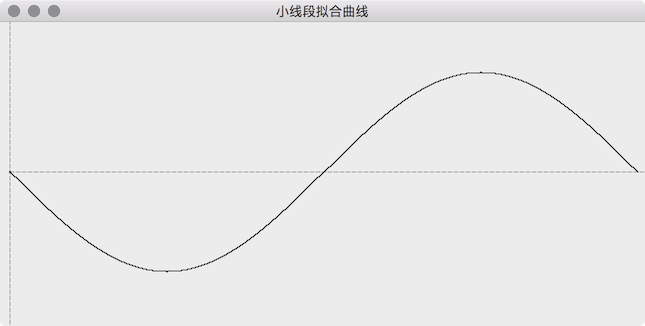
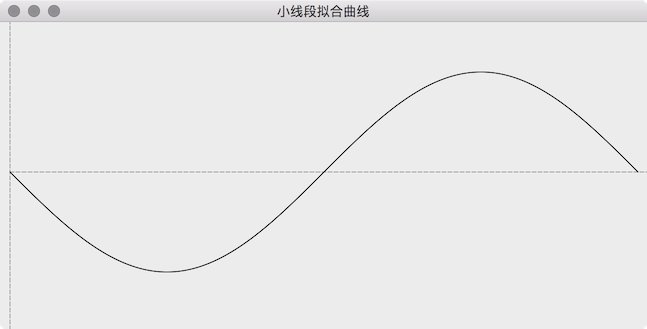
虽然绘制出了正弦曲线,但是看上去全是锯齿,效果很不理想,可以用算法拟合得效果更好,但不是专业搞图形学的人估计很困难,至少我目前不具备这样的能力。一次很意外的发现,QPainterPath 把很短的线段连成曲线时会自动的处理得很平滑,把上面的实现改为用 QPainterPath,效果如下,正是我们想要的:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| void FittingCurveWidget::paintEvent(QPaintEvent *) {
QPainter painter(this);
painter.setRenderHint(QPainter::Antialiasing);
painter.translate(10, 150);
painter.setPen(QPen(Qt::gray, 1, Qt::DashLine));
painter.drawLine(0, 0, 700, 0);
painter.drawLine(0, -200, 0, 200);
QPainterPath path(QPointF(0, 0));
for (int i = 0; i <= 628; ++i) {
qreal x = i;
qreal y = qSin(i/314.0*M_PI) * 100;
path.lineTo(x, y);
}
painter.setPen(QPen(Qt::black, 1));
painter.drawPath(path);
}
|
使用线段拟合曲线其实也不难嘛,是不是迫不及待的想自己实现一下怎么绘制余弦曲线了?了解了实现原理,甚至于更复杂的曲线例如 y=x^3-5x+4 都难不住我们了。


