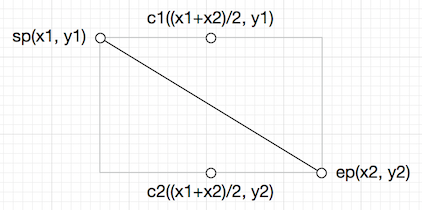Content Table
2016-12-11

绘制平滑曲线

得到曲线上的点，画出曲线，这是一个很常见的需求。画曲线嘛，当然难不住我们，用 QPainter::drawLine() 把曲线上的点连起来不就好了？So easy，轻轻松松搞定，开开心心的交任务去了。

正在聚精会神炒股的老板一瞅，气不打一处来：“你这画的是什么鬼，这个线直来直去的，太不专业了”，抬头指着屏幕上的炒股软件，瞅着迷离的眼神：“看看人家的这个曲线，就像少女的皮肤般那么的柔顺、平滑”，口气马上一百八十度大转弯：“在看看你的，像八十岁老头的那样全是褶皱！” 擦完脸上的口水，赶快想办法去吧。

创建平滑曲线，有很多种方式，可以使用现成的库，例如 QWT，QCustomPlot 等，也可以研究平滑曲线的理论，实现平滑曲线的插值函数。这里我们提供二个实现，利用 QPainterPath，根据曲线上的点创建平滑曲线，他们各有利弊，使用分三步：

1
2
3
4
5
6
7
8
9
10
11
12
13
// [1] 把曲线上的点放到 QList 里
QList<QPointF> knots;
knots << QPointF(x1, y1);
...
knots << QPointF(xn, yn);

// [2] 创建平滑曲线
QPainterPath smoothCurve1 = SmoothCurveGenerator1::generateSmoothCurve(knots);
QPainterPath smoothCurve2 = SmoothCurveGenerator2::generateSmoothCurve(knots);

// [3] 绘制曲线
painter.drawPath(smoothCurve1);
painter.drawPath(smoothCurve2);

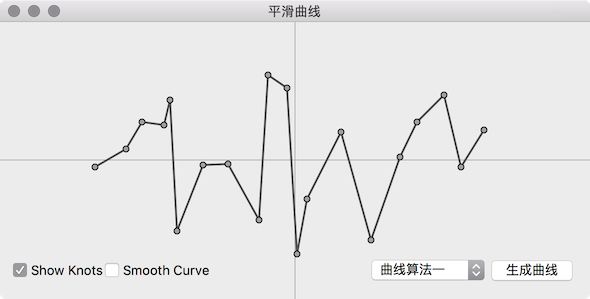
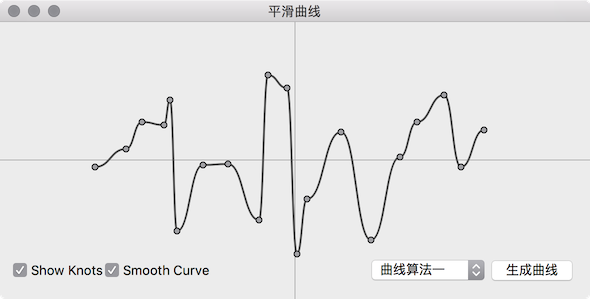
最后画出来的曲线效果如下，这次应该不会被喷了吧：


Qt 中可以使用 QPainterPath::cubicTo() 函数实现绘制平滑曲线，绘制平滑曲线的关键是控制点的计算，sp 为线段的起始点，ep 为线段的终点，c1，c2 为贝塞尔曲线的控制点，其坐标计算如下

类 SmoothCurveGenerator1 使用上面的原理生成平滑曲线

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#ifndef SMOOTHCURVEGENERATOR1_H
#define SMOOTHCURVEGENERATOR1_H

#include <QList>
#include <QPointF>
#include <QPainterPath>

class SmoothCurveGenerator1 {
public:
    /**
     * 传入曲线上的点的 list，创建平滑曲线
     *
     * @param points - 曲线上的点
     * @return - 返回使用给定的点创建的 QPainterPath 表示的平滑曲线
     */
    static QPainterPath generateSmoothCurve(const QList<QPointF> &points);
};

#endif // SMOOTHCURVEGENERATOR1_H
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include "SmoothCurveGenerator1.h"

QPainterPath SmoothCurveGenerator1::generateSmoothCurve(const QList<QPointF> &points) {
    if (points.size() == 0) {
        return QPainterPath();
    }

    QPainterPath path(points[0]);

    for (int i = 0; i < points.size() - 1; ++i) {
        // 控制点的 x 坐标为 sp 与 ep 的 x 坐标和的一半
        // 第一个控制点 c1 的 y 坐标为起始点 sp 的 y 坐标
        // 第二个控制点 c2 的 y 坐标为结束点 ep 的 y 坐标
        QPointF sp = points[i];
        QPointF ep = points[i+1];
        QPointF c1 = QPointF((sp.x() + ep.x()) / 2, sp.y());
        QPointF c2 = QPointF((sp.x() + ep.x()) / 2, ep.y());
        path.cubicTo(c1, c2, ep);
    }

    return path;
}

接下来就介绍一下生成平滑曲线的具体使用方法，就是开头被喷的那个曲线图的平滑实现。

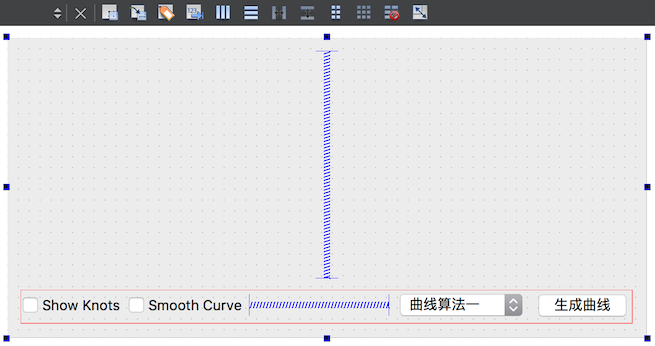
在 SmoothCurveWidget.ui 上如图放两个 QCheckBox，命名为 showKnotsCheckBox 和 showSmoothCurveCheckBox，QPushButton 用于点击重新生成曲线，ComboBox 用于选择生成曲线的算法：

下面是 SmoothCurveWidget.h, SmoothCurveWidget.cpp 和 main.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#ifndef SMOOTHCURVEWIDGET_H
#define SMOOTHCURVEWIDGET_H

#include <QWidget>
#include <QList>
#include <QPointF>
#include <QPainterPath>

namespace Ui {
class SmoothCurveWidget;
}

class SmoothCurveWidget : public QWidget {
    Q_OBJECT

public:
    explicit SmoothCurveWidget(QWidget *parent = 0);
    ~SmoothCurveWidget();

protected:
    void paintEvent(QPaintEvent *event) Q_DECL_OVERRIDE;

private slots:
    void generateCurves(); // 生成平滑曲线和非平滑曲线

private:
    Ui::SmoothCurveWidget *ui;
    QList<QPointF> knots;        // 曲线上的点
    QPainterPath smoothCurve1;   // 平滑曲线
    QPainterPath smoothCurve2;   // 平滑曲线
    QPainterPath nonSmoothCurve; // 直接连接点的非平滑曲线
};

#endif // SMOOTHCURVEWIDGET_H
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include "SmoothCurveWidget.h"
#include "ui_SmoothCurveWidget.h"
#include "SmoothCurveGenerator1.h"
#include "SmoothCurveGenerator2.h"

#include <QPainter>
#include <QtGlobal>
#include <QDateTime>

SmoothCurveWidget::SmoothCurveWidget(QWidget *parent) :
    QWidget(parent), ui(new Ui::SmoothCurveWidget) {
    ui->setupUi(this);

    connect(ui->generateCurveButton, SIGNAL(clicked(bool)), this, SLOT(generateCurves()));
    connect(ui->showKnotsCheckBox, SIGNAL(clicked(bool)), this, SLOT(update()));
    connect(ui->showSmoothCurveCheckBox, SIGNAL(clicked(bool)), this, SLOT(update()));
    connect(ui->smoothCurveGeneratorComboBox, SIGNAL(currentIndexChanged(int)), this, SLOT(update()));

    ui->generateCurveButton->click();
}

SmoothCurveWidget::~SmoothCurveWidget() {
    delete ui;
}

void SmoothCurveWidget::paintEvent(QPaintEvent *) {
    QPainter painter(this);
    painter.setRenderHint(QPainter::Antialiasing);
    painter.translate(width() / 2 , height() / 2);
    painter.scale(1, -1);

    // 画坐标轴
    painter.setPen(QColor(180, 180, 180));
    painter.drawLine(-500, 0, 500, 0);
    painter.drawLine(0, 500, 0, -500);

    // showSmoothCurveCheckBox 被选中时显示平滑曲线，否则显示非平滑曲线
    painter.setPen(QPen(QColor(80, 80, 80), 2));
    if (ui->showSmoothCurveCheckBox->isChecked() && ui->smoothCurveGeneratorComboBox->currentIndex() == 0) {
        painter.drawPath(smoothCurve1);
    } else if (ui->showSmoothCurveCheckBox->isChecked() && ui->smoothCurveGeneratorComboBox->currentIndex() == 1) {
        painter.drawPath(smoothCurve2);
    } else {
        painter.drawPath(nonSmoothCurve);
    }

    // 如果曲线上的点可见，则显示出来
    if (ui->showKnotsCheckBox->isChecked()) {
        painter.setPen(Qt::black);
        painter.setBrush(Qt::gray);
        foreach(QPointF p, knots) {
            painter.drawEllipse(p, 3, 3);
        }
    }
}

void SmoothCurveWidget::generateCurves() {
    qsrand(QDateTime::currentDateTime().toMSecsSinceEpoch());

    // 随机生成曲线上的点: 横坐标为 [-200, 200]，纵坐标为 [-100, 100]
    int x = -200;
    knots.clear();
    while (x < 200) {
        knots << QPointF(x, qrand() % 200 - 100);
        x += qMin(qrand() % 30 + 5, 200);
    }

    // 根据曲线上的点创建平滑曲线
    smoothCurve1 = SmoothCurveGenerator1::generateSmoothCurve(knots);
    smoothCurve2 = SmoothCurveGenerator2::generateSmoothCurve(knots);

    // 连接点创建非平滑曲线曲线
    nonSmoothCurve = QPainterPath();
    nonSmoothCurve.moveTo(knots[0]);
    for (int i = 1; i < knots.size(); ++i) {
        nonSmoothCurve.lineTo(knots[i]);
    }

    update();
}
1
2
3
4
5
6
7
8
9
10
11
#include "SmoothCurveWidget.h"
#include <QApplication>

int main(int argc, char *argv[]) {
    QApplication a(argc, argv);

    SmoothCurveWidget w;
    w.show();

    return a.exec();
}

为了让程序更具有普谝性，曲线上的点采用随机生成，所以每次生成的曲线是不一样的，选中 “Smooth Curve” 时显示为平滑曲线，没有选中则显示为非平滑的曲线。选中 “Show knots” 显示曲线上的点，反之则不显示。

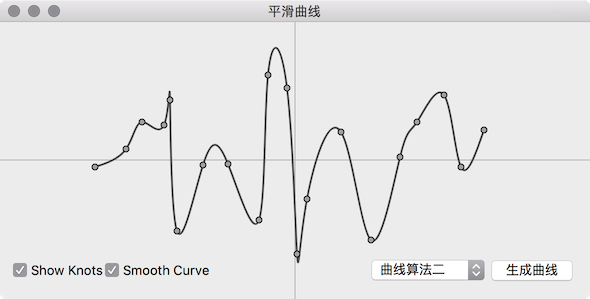
如果仔细观察 SmoothCurveGenerator1 生成的平滑曲线，会发现平滑曲线段之间会有很多小段的抖动，下面提供另一个也是使用 QPainterPath 实现平滑曲线的方法，可以解决平滑曲线段之间的抖动问题，但是曲线段在比较陡时，曲线上的值可能会超出曲线原来值的范围，但是总体上看效果更好，改编自 http://www.codeproject.com/Articles/31859/Draw-a-Smooth-Curve-through-a-Set-of-D-Points-wit，核心是使用曲线上的点计算出贝塞尔曲线的两个控制点，然后使用贝塞尔曲线生成平滑曲线，很惭愧的是生成控制点的算法细节我没看懂，只不过是作了一次搬运工，把程序移植到了 Qt 上，有兴趣的话，请自行参考吧，不过即使没有理解控制点的生成算法也不影响使用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#ifndef SMOOTHCURVEGENERATOR2_H
#define SMOOTHCURVEGENERATOR2_H

#include <QList>
#include <QPointF>
#include <QPainterPath>

class SmoothCurveGenerator2 {
public:
    /**
     * 传入曲线上的点的 list，创建平滑曲线
     * @param points - 曲线上的点
     * @return - 返回使用给定的点创建的 QPainterPath 表示的平滑曲线
     */
    static QPainterPath generateSmoothCurve(const QList<QPointF> &points);

private:
    /**
     * Solves a tridiagonal system for one of coordinates (x or y)
     * of first Bezier control points.
     * @param result - Solution vector.
     * @param rhs - Right hand side vector.
     * @param n - Size of rhs.
     */
    static void calculateFirstControlPoints(double * &result, const double *rhs, int n);

    /**
     * Calculate control points of the smooth curve using the given knots.
     * @param knots - Points of the given curve.
     * @param firstControlPoints - Store the generated first control points.
     * @param secondControlPoints - Store the generated second control points.
     */
    static void calculateControlPoints(const QList<QPointF> &knots,
                                       QList<QPointF> *firstControlPoints,
                                       QList<QPointF> *secondControlPoints);
};

#endif // SMOOTHCURVEGENERATOR2_H
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#include "SmoothCurveGenerator2.h"

QPainterPath SmoothCurveGenerator2::generateSmoothCurve(const QList<QPointF> &points) {
    QPainterPath path;
    int len = points.size();

    if (len < 2) {
        return path;
    }

    QList<QPointF> firstControlPoints;
    QList<QPointF> secondControlPoints;
    calculateControlPoints(points, &firstControlPoints, &secondControlPoints);

    path.moveTo(points[0].x(), points[0].y());

    // Using bezier curve to generate a smooth curve.
    for (int i = 0; i < len - 1; ++i) {
        path.cubicTo(firstControlPoints[i], secondControlPoints[i], points[i+1]);
    }

    return path;
}

void SmoothCurveGenerator2::calculateFirstControlPoints(double *&result, const double *rhs, int n) {
    result = new double[n];
    double *tmp = new double[n];
    double b = 2.0;
    result[0] = rhs[0] / b;

    // Decomposition and forward substitution.
    for (int i = 1; i < n; i++) {
        tmp[i] = 1 / b;
        b = (i < n - 1 ? 4.0 : 3.5) - tmp[i];
        result[i] = (rhs[i] - result[i - 1]) / b;
    }

    for (int i = 1; i < n; i++) {
        result[n - i - 1] -= tmp[n - i] * result[n - i]; // Backsubstitution.
    }

    delete[] tmp;
}

void SmoothCurveGenerator2::calculateControlPoints(const QList<QPointF> &knots,
                                                   QList<QPointF> *firstControlPoints,
                                                   QList<QPointF> *secondControlPoints) {
    int n = knots.size() - 1;

    for (int i = 0; i < n; ++i) {
        firstControlPoints->append(QPointF());
        secondControlPoints->append(QPointF());
    }

    if (n == 1) {
        // Special case: Bezier curve should be a straight line.
        // P1 = (2P0 + P3) / 3
        (*firstControlPoints)[0].rx() = (2 * knots[0].x() + knots[1].x()) / 3;
        (*firstControlPoints)[0].ry() = (2 * knots[0].y() + knots[1].y()) / 3;

        // P2 = 2P1 – P0
        (*secondControlPoints)[0].rx() = 2 * (*firstControlPoints)[0].x() - knots[0].x();
        (*secondControlPoints)[0].ry() = 2 * (*firstControlPoints)[0].y() - knots[0].y();

        return;
    }

    // Calculate first Bezier control points
    double *xs = 0;
    double *ys = 0;
    double *rhsx = new double[n]; // Right hand side vector
    double *rhsy = new double[n]; // Right hand side vector

    // Set right hand side values
    for (int i = 1; i < n - 1; ++i) {
        rhsx[i] = 4 * knots[i].x() + 2 * knots[i + 1].x();
        rhsy[i] = 4 * knots[i].y() + 2 * knots[i + 1].y();
    }
    rhsx[0] = knots[0].x() + 2 * knots[1].x();
    rhsx[n - 1] = (8 * knots[n - 1].x() + knots[n].x()) / 2.0;
    rhsy[0] = knots[0].y() + 2 * knots[1].y();
    rhsy[n - 1] = (8 * knots[n - 1].y() + knots[n].y()) / 2.0;

    // Calculate first control points coordinates
    calculateFirstControlPoints(xs, rhsx, n);
    calculateFirstControlPoints(ys, rhsy, n);

    // Fill output control points.
    for (int i = 0; i < n; ++i) {
        (*firstControlPoints)[i].rx() = xs[i];
        (*firstControlPoints)[i].ry() = ys[i];

        if (i < n - 1) {
            (*secondControlPoints)[i].rx() = 2 * knots[i + 1].x() - xs[i + 1];
            (*secondControlPoints)[i].ry() = 2 * knots[i + 1].y() - ys[i + 1];
        } else {
            (*secondControlPoints)[i].rx() = (knots[n].x() + xs[n - 1]) / 2;
            (*secondControlPoints)[i].ry() = (knots[n].y() + ys[n - 1]) / 2;
        }
    }

    delete xs;
    delete ys;
    delete[] rhsx;
    delete[] rhsy;
}

相信还有其他用于生成平滑曲线的方法，甚至可以同时解决 SmoothCurveGenerator1 和 SmoothCurveGenerator2 的问题，这个需要大家继续深入的研究了。