图-最短路径-Dijkstra

求图中一点到其他点的最短路径可使用 Dijkstra 算法 (使用广度优先策略):

• 使用优先级队列实现找最小权重的点 (数组遍历也可以)
• 前驱节点数组
• 权重节点数组 (已访问节点)
• 连接表的存储: Map<String, List<String>>: key 为节点名字，List 为邻接表

A* 算法是 Dijkstra 算法的高级版，计算权重的时候点的权重加上点到目标的估算值: f(n) = g(n) + h(n)，而 Dijkstra 则为 f(n) = g(n)

package graph;

import com.alibaba.fastjson.JSON;
import lombok.Getter;
import lombok.Setter;
import lombok.experimental.Accessors;

import java.util.*;

/**
 * 迪杰斯特拉算法求一点到其他所有点的最短路径
 */
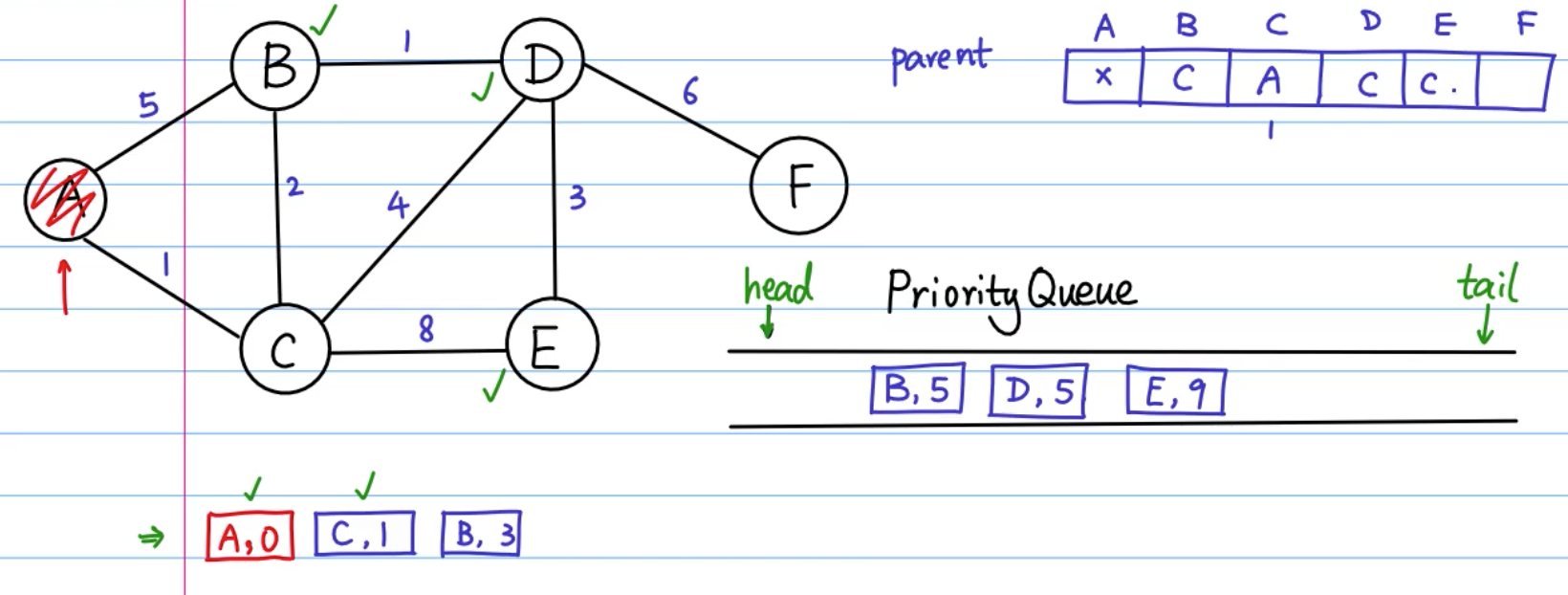
public class Dijkstra {
    public static void main(String[] args) {
        // 1. 把起点加入到队列
        // 2. 队列中距离最小的顶点出队 (min)
        // 3. 未访问过的顶点标记为已访问，忽略被访问过的顶点 (添加到访问过的节点)
        // 4. 遍历 min 的所有未访问过的临接点，调整其距离为 weight + min.distance，并加入优先级队列
        // 5. 直到队列为空结束循环

        Graph graph = Graph.build("A-B:16,B-C:10,C-D:3,D-E:4,E-F:8,F-A:14,B-G:7,C-G:6,E-G:2,F-G:9,A-G:12,C-E:5");
        Map<String, Entry> visited = new HashMap<>(); // 访问过的顶点
        PriorityQueue<Entry> queue = new PriorityQueue<>(Comparator.comparing(Entry::getDistance)); // 优先级队列，距离小的先出队

        // [1] 把起点加入到队列
        String startVertex = "C";
        queue.offer(new Entry(startVertex, null, 0));

        while (!queue.isEmpty()) {
            // [2] 队列中距离最小的顶点出队
            Entry min = queue.poll();
            String currentVertex = min.getVertex();

            // [3] 未访问过的顶点标记为已访问，忽略被访问过的顶点 (添加到访问过的节点)
            if (visited.containsKey(currentVertex)) {
                continue;
            }

            // 添加到访问过的节点
            visited.put(currentVertex, min);

            // [4] 遍历 min 的所有未访问过的临接点，调整其距离为 weight + min.distance，并加入优先级队列
            for (Graph.Edge edge : graph.getVertexEdges(currentVertex)) {
                // 忽略访问过的顶点
                if (visited.containsKey(edge.getEnd())) {
                    continue;
                }

                queue.offer(new Entry(edge.getEnd(), currentVertex, edge.getWeight() + min.getDistance()));
            }
        }

        // 输出最短距离的顶点信息，可以得到起点到它的距离、前驱
        System.out.println(JSON.toJSONString(visited, true));

        // 输出起点到其他点的最短路径
        for (String vertex : graph.getVertices()) {
            System.out.printf("\n最短路径: %s 到 %s，距离 %.2f\n", startVertex, vertex, visited.get(vertex).getDistance());

            List<String> path = new LinkedList<>();
            Entry current = visited.get(vertex);
            while (current != null) {
                path.add(0, current.getVertex());
                current = visited.get(current.getPrevVertex());
            }
            System.out.println(String.join("->", path));
        }
    }

    @Getter
    @Setter
    @Accessors(chain = true)
    public static class Entry {
        String vertex;     // 顶点
        String prevVertex; // 前驱
        double distance;   // 距离

        public Entry(String vertex, String prevVertex, double distance) {
            this.vertex     = vertex;
            this.prevVertex = prevVertex;
            this.distance   = distance;
        }
    }
}

输出:

{
    "A":{
        "distance":18.0,
        "prevVertex":"G",
        "vertex":"A"
    },
    "B":{
        "distance":10.0,
        "prevVertex":"C",
        "vertex":"B"
    },
    "C":{
        "distance":0.0,
        "vertex":"C"
    },
    "D":{
        "distance":3.0,
        "prevVertex":"C",
        "vertex":"D"
    },
    "E":{
        "distance":5.0,
        "prevVertex":"C",
        "vertex":"E"
    },
    "F":{
        "distance":13.0,
        "prevVertex":"E",
        "vertex":"F"
    },
    "G":{
        "distance":6.0,
        "prevVertex":"C",
        "vertex":"G"
    }
}

最短路径: C 到 A，距离 18.00
C->G->A

最短路径: C 到 B，距离 10.00
C->B

最短路径: C 到 C，距离 0.00
C

最短路径: C 到 D，距离 3.00
C->D

最短路径: C 到 E，距离 5.00
C->E

最短路径: C 到 F，距离 13.00
C->E->F

最短路径: C 到 G，距离 6.00
C->G