Content Table
2020-02-23

图-最小生成树-Kruskal

最小生成树 (Minumum Cost Spanning Tree，简称 MST) 的 2 个经典算法:

  • Prim (普里姆算法): 从顶点出发
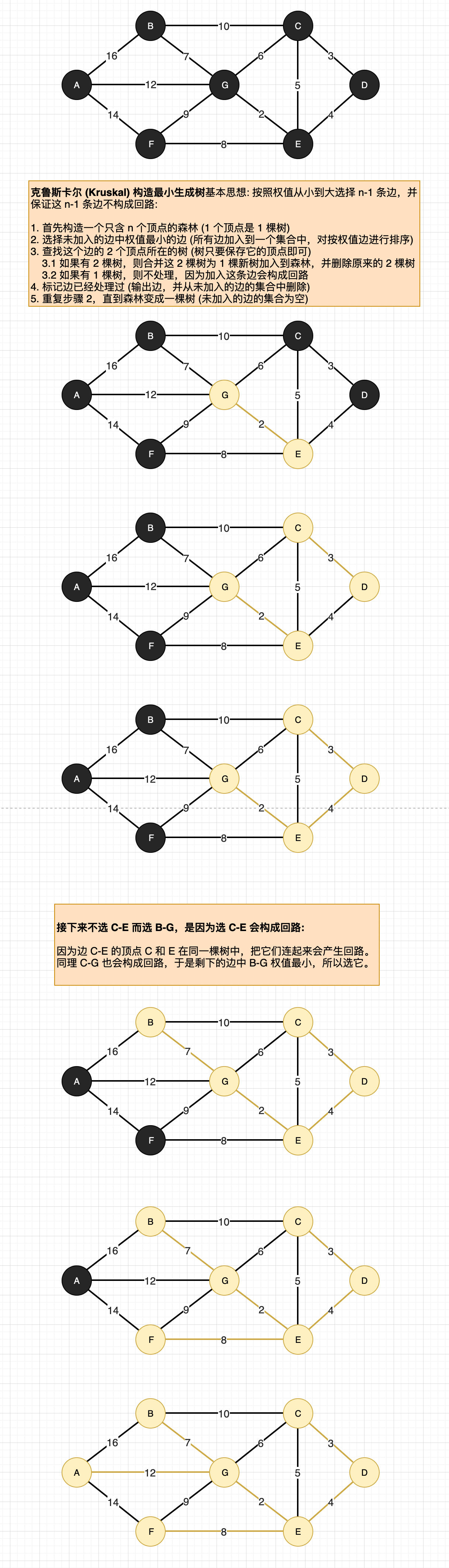
  • Kruskal (克鲁斯卡尔算法): 从边出发

网: 带权无向图
最小生成树: 在包含 n 个顶点的连通图中，找出只有 (n-1) 条边，包含所有 n 个顶点的连通子图，也就是所谓的极小连通子图

下面图解 Prim 算法生成最小生成树的过程:

Kruskal 算法的代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
package graph;

import com.alibaba.fastjson.JSON;

import java.util.*;

/**
 * 克鲁斯卡尔算法生成最小生成树，从边出发
 */
public class Kruskal {
    public static void main(String[] args) {
        // 1. 构造只包含 n 个顶点的森林
        // 2. 把图的边按照从小到大排列
        // 3. 选择未加入的边中权值最小的边
        // 4. 查找这条边的 2 个顶点所在的树
        //    4.1 如果有 2 棵树，则合并这两颗树为一颗新树加入到森林，并删除原来的 2 棵树，这条边为最小生成树的边
        //    4.1 如果有 1 棵树，则不处理，因为加入这条边会构成森林
        // 5. 标记边已经处理过，从未加入的边中删除
        // 6. 重复步骤 2，直到森林变成一棵树

        Graph graph = Graph.build("A-B:16,B-C:10,C-D:3,D-E:4,E-F:8,F-A:14,B-G:7,C-G:6,E-G:2,F-G:9,A-G:12,C-E:5");

        // [1] 构造只包含 n 个顶点的森林
        List<Set<String>> forest = new LinkedList<>();
        for (String vertex : graph.getVertices()) {
            Set<String> tree = new HashSet<>();
            tree.add(vertex);
            forest.add(tree);
        }

        // [2] 把图的边按照从小到大排列
        List<Graph.Edge> edges = new LinkedList<>(graph.getEdges());
        edges.sort(Comparator.comparing(Graph.Edge::getWeight));

        // [6] 直到森林变成一棵树
        while (forest.size() > 1) {
            // [3] 选择未加入的边中权值最小的边
            // [5] 标记边已经处理过，从未加入的边中删除
            Graph.Edge edge = edges.remove(0);

            // [4] 查找这条边的 2 个顶点所在的树
            Set<String> tree1 = Kruskal.findTreeOfVertex(forest, edge.getStart());
            Set<String> tree2 = Kruskal.findTreeOfVertex(forest, edge.getEnd());

            // [4.1] 如果有 2 棵树，则合并这两颗树为一颗新树加入到森林，并删除原来的 2 棵树，这条边为最小生成树的边
            if (tree1 != tree2) {
                Set<String> tree = new HashSet<>();
                tree.addAll(tree1);
                tree.addAll(tree2);
                forest.remove(tree1);
                forest.remove(tree2);
                forest.add(tree);

                // 最小生成树的边
                System.out.println(JSON.toJSONString(edge));
            }
        }
    }

    /**
     * 查找森林中包含顶点 vertex 的树
     *
     * @param forest 森林
     * @param vertex 要查找的顶点
     * @return 返回查找到的树
     */
    public static Set<String> findTreeOfVertex(List<Set<String>> forest, String vertex) {
        for (Set<String> tree : forest) {
            if (tree.contains(vertex)) {
                return tree;
            }
        }

        return null;
    }
}