图-最小生成树-Prim

最小生成树 (Minumum Cost Spanning Tree，简称 MST) 的 2 个经典算法:

• Prim (普里姆算法): 从顶点出发
• Kruskal (克鲁斯卡尔算法): 从边出发

网: 带权无向图
最小生成树: 在包含 n 个顶点的连通图中，找出只有 (n-1) 条边，包含所有 n 个顶点的连通子图，也就是所谓的极小连通子图

普里姆 (Prim) 算法求最小生成树算法如如下:

1. 设 G = (V, E) 是联通网，T = (U, D) 是最小生成树，V, U 是顶点集合，E, D 是边的集合
2. 若从顶点 u 开始构造最小生成树，则从集合 V 中取出顶点 u 放入集合 U 中，标记顶点 u 被访问过了: visited[u] = 1
3. 若集合 U 中顶点 ui 与集合 V-U 中的顶点 vj 之间存在边，则寻找这些边中权值最小的边，但不能构成回路，将顶点 vj 加入集合 U 中，将边 (ui, vj) 加入集合 D 中，标记 visited[vj] = 1
4. 重复步骤 3，直到 U 与 V 相等，即所有顶点都被标记为访问过，此时 D 中有 n-1 条边

不管从哪一个顶点开始构建最小生成树，最后得到的最小生成树的边的权值加起来都相等。

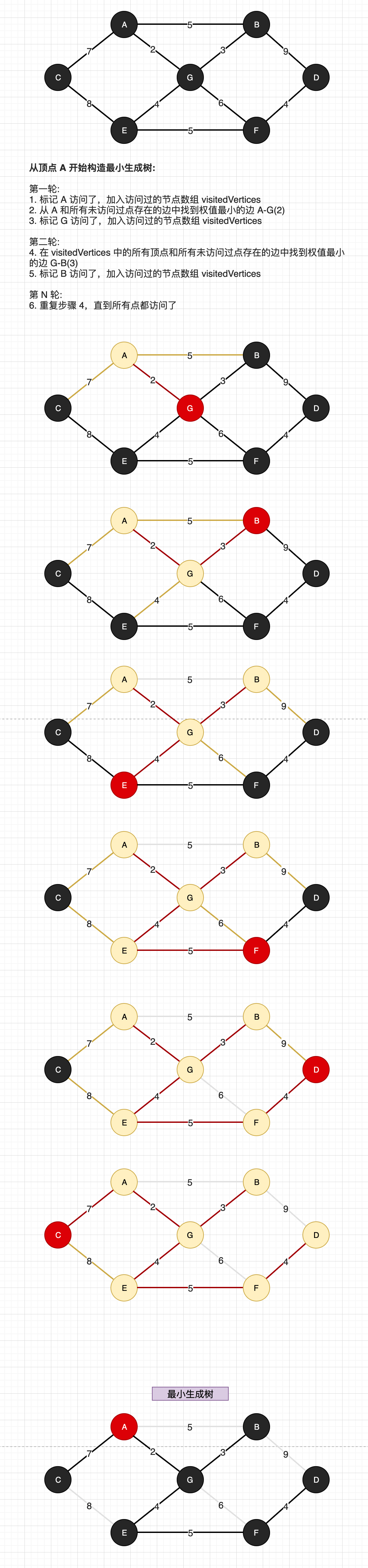
下面图解 Prim 算法生成最小生成树的过程，其中:

• 黑色节点表示未访问过节点
• 黄色节点表示已访问过节点
• 红色节点表示未访问过，但是将选择为访问的节点
• 红色的边为最小生成树中的边
• 灰色的边为不需要在判断的边，因为它的 2 个顶点都访问过了
• 黄色的边，其有 1 个顶点被访问过了，另一个顶点未被访问

Prim 算法的代码:

package graph;

import com.alibaba.fastjson.JSON;

import java.util.HashSet;
import java.util.Set;

/**
 * 普鲁姆算法生成最小生成树，从顶点出发
 */
public class Prim {
    public static void main(String[] args) {
        // 1. 把图的顶点放到集合 unmstVertices 中
        // 2. 最小生成树的顶点放到集合 mstVertices 中
        // 3. 指定一个顶点，从它开始构建最小生成树
        // 4. 从最小生成树中的节点的边中找到符合要求的边: 一个顶点在 mstVertices 中，另一个顶点在 unmstVertices 中，并且在这些边中权值最小
        // 5. 把 4 中找到的边加入到最小生成树，且从 unmstVertices 中删除这条边的顶点
        // 6. 重复步骤 4，直到所有点都加入 mstVertices，即 unmstVertices 为空

        Graph graph = Graph.build("A-B:16,B-C:10,C-D:3,D-E:4,E-F:8,F-A:14,B-G:7,C-G:6,E-G:2,F-G:9,A-G:12,C-E:5");
        Set<String> unmstVertices = new HashSet<>(graph.getVertices()); // 非最小生成树的顶点
        Set<String> mstVertices   = new HashSet<>(); // 最小生成树的节点

        // [3] 指定一个顶点，从它开始构建最小生成树
        mstVertices.add("E");
        unmstVertices.remove("E");

        while (!unmstVertices.isEmpty()) {
            Graph.Edge minEdge = null;
            double minWeight   = Double.MAX_VALUE;

            // [4] 从最小生成树中的节点的边中找到符合要求的边: 一个顶点在 mstVertices 中，另一个顶点在 unmstVertices 中，并且在这些边中权值最小
            for (String vertex : mstVertices) {
                for (Graph.Edge edge : graph.getVertexEdges(vertex)) {
                    String end = edge.getEnd();

                    // 边的另一个顶点在 unmstVertices 中，并且在这些边中权值最小
                    if (unmstVertices.contains(end) && edge.getWeight() < minWeight) {
                        minEdge   = edge;
                        minWeight = edge.getWeight();
                    }
                }
            }

            // [5] 把 4 中找到的边加入到最小生成树，且从 unmstVertices 中删除这条边的顶点
            // 每次肯定能找到一条边加入最小生成树
            mstVertices.add(minEdge.getEnd());
            unmstVertices.remove(minEdge.getEnd());
            System.out.println(JSON.toJSONString(minEdge));
        }
    }
}